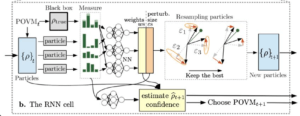
Noise and its control in quantum computing systems
After more than two decades of working towards building a computer based on quantum mechanical principles, a basic obstacle remains: noise. Noise-suppression techniques have shown encouraging progress over the years, but the noise threshold below which useful, reliable computation can be accomplished is still far from attainable. We seek better understanding of the physical nature of the noise affecting quantum information processing (QIP) tasks beyond the naive quantum-channel description, and examine the efficacy of error correction and fault-tolerant schemes for different types of noise, different practical QIP tasks, and in different physical implementations of quantum computing components. Of particular recent interest is the goal of bringing the ideas of quantum error correction and fault tolerance from abstract theory towards actual realisation in near-term quantum devices, and to examine the practical resource costs of doing error correction for large-scale reliable quantum computation.
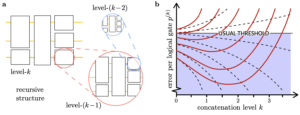
Limitations to quantum computing from resource constraints [from Fellous-Asiani et al. PRX Quantum 2, 040335 (2021)].
This direction of research is supported by a CQT Fellowship, a Tier-2 grant (Ministry of Education Singapore), and an NRF-ANR Singapore-France joint grant.
Relevant publications:
- J Qi, X Xu, D Poletti, and HK Ng, Efficacy of noisy dynamical decoupling, Phys Rev A 107, 032615 (2023); arXiv:2209.9039(2022).
- (Preprint) M Fellous-Asiani, JH Chai, Y Thonnart, HK Ng, RS Whitney, and A Auffèves, Optimizing resource efficiencies for scalable full-stack quantum computers, arXiv:2209.05469 (2022).
- A Jayashankar, My DHL, HK Ng, and P Mandayam, Achieving fault tolerance against amplitude-damping noise, Phys Rev Research 4, 023034 (2022); arXiv:2107.05485.
- M Fellous-Asiani, JH Chai, RS Whitney, A Auffèves, and HK Ng, Limitations in quantum computing from resource constraints, PRX Quantum 2, 040335 (2021); arXiv:2007.01966.
- A Jayashankar, AM Babu, HK Ng, and P Mandayam, Finding good codes using the Cartan form, Phys Rev A 101, 042307 (2020); arXiv:1911.02965.
Selected past works of relevance:
- YL Len and HK Ng, Open-system quantum error correction, Phys Rev A 98, 022307(2018); arXiv:1804:09486.
- HK Ng, DA Lidar, and J Preskill, Combining dynamical decoupling with fault-tolerant quantum computation, Phys Rev A 84, 012305 (2011).
- HK Ng and P Mandayam, Simple approach to approximate quantum error correction based on the transpose channel, Phys Rev A 81, 062342 (2010).
- HK Ng and J Preskill, Fault-tolerant quantum computation versus Gaussian noise, Phys Rev A 79, 032318 (2009).
Estimating relevant noise parameters
An essential input to effective noise-suppression strategies is the nature of the noise that afflicts the quantum system. Here, we seek to advance methods for the practical characterization of noise in quantum systems, through better use of limited data from resource-expensive standard process tomography, as well as direct measurements of noise parameters relevant for high-fidelity QIP tasks.
Adaptive quantum tomography aided by neural networks [from Quek et al., arXiv:1812.06693]
- Y Quek, S Fort, and HK Ng, Adaptive Quantum State Tomography with Neural Networks, npj Quantum Inf 7, 105 (2021); arXiv:1812.06693.
- Y Gu, R Mishra, B-G Englert, and HK Ng, Randomized linear gate set tomography, PRX Quantum 2, 030328 (2021); arXiv:2010.12235.
- J Qi and HK Ng, Randomized benchmarking in the presence of time-correlated dephasing noise, Phys Rev A 103, 022607 (2021); arXiv:2010.11498.
- Y Lu, JY Sim, J Suzuki, B-G Englert, and HK Ng, Direct estimation of minimum gate fidelity, Phys Rev A 102, 022410 (2020); arXiv:2004.02422.
- Y Gazit, HK Ng, and J Suzuki, Quantum process tomography via optimal design of experiments, Phys Rev A 100, 012350 (2019); arXiv:1904.11849.
- J Qi and HK Ng, Comparing the randomized benchmarking figure with the average infidelity of a quantum gate-set, Int J Quant Inf 17, 1950031 (2019); arXiv:1805.10622.
- J Shang, HK Ng, A Sehrawat, X Li, and B-G Englert, Optimal error regions for quantum state estimation, New J Phys 15, 123026 (2013); arXiv:1302.4081.